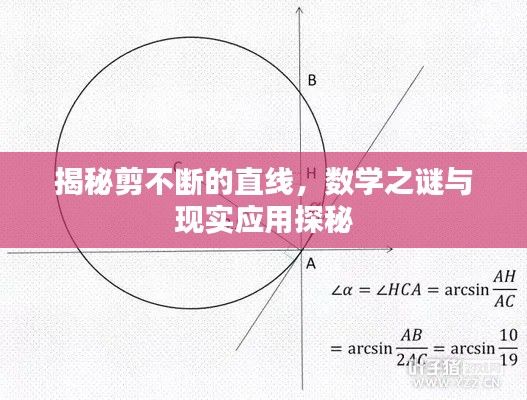
当我们谈论几何学和数学时，一种常见的概念是直线，直线是一种基本的几何元素，通常被描述为无限延伸、无弯曲的路径，有一个有趣的问题：是否存在一种“剪不断的直线”？这个问题似乎挑战了我们对直线的基本理解，但实际上，它引导我们深入探讨数学的深度和广度。

我们来探讨这个问题的数学背景，在数学中，直线被定义为一种无限延伸的、无弯曲的几何图形，在传统的几何概念中，直线是连续的，没有断点或弯曲点，因此理论上无法被“剪断”，如果我们从非传统几何学的角度思考，例如分形几何或量子几何，可能会发现一些特殊的直线模型，它们可能在微观尺度上呈现出不同的特性，这些理论中的直线可能具有某种“剪不断”的特性，但这需要更深入的理论研究和验证。

当我们转向现实世界的物理应用时，“剪不断的直线”这个概念可能有了新的解读，在材料科学中，某些特殊的材料如玻璃、金属等，尽管可以被切割和断裂，但在宏观尺度上，它们仍然表现出连续性和直线的特性，光纤通信技术中的光线传播也可以被看作是“剪不断的直线”，光线在光纤中传播时，尽管经历了多次反射和折射，但在宏观尺度上，我们可以将其看作是一条连续的直线。

“剪不断的直线”这个概念还可以被应用于其他领域，在生物学中，某些细胞结构或分子链可能表现出某种程度的“剪不断”特性，在计算机科学中，算法和数据处理中的某些路径或轨迹也可能需要保持连续性和不可中断性，这些例子展示了“剪不断的直线”在现实世界的多样性和广泛性。

“剪不断的直线是什么”这个问题是一个富有挑战性的数学问题，它引导我们深入探讨数学的深度和广度，这个问题在现实世界中也有广泛的应用，通过深入研究这个问题，我们可以更好地理解数学与现实世界的联系，发现新的科学和技术应用。

从数学的角度来看，“剪不断的直线”可能涉及到更深入的几何理论，如分形几何和量子几何等，这些理论为我们提供了一种新的视角来看待直线的性质和行为，通过深入研究这些理论，我们可能会发现一些新的直线模型，它们在微观尺度上表现出与传统几何不同的特性。

从现实世界的角度来看，“剪不断的直线”这个概念可以应用于许多领域，在材料科学中，某些材料的连续性和直线特性对于工程应用至关重要，在生物学和医学中，细胞结构和分子链的连续性可能对于生命活动有着重要影响，在计算机科学和信息技术中，“剪不断的直线”的概念也可以被用于描述数据处理和算法中的路径和轨迹的连续性，这些应用展示了数学与现实世界的紧密联系和相互影响。

“剪不断的直线是什么”这个问题是一个富有挑战性的数学问题，它引导我们深入探讨数学的深度和广度，这个问题也具有广泛的应用价值，通过深入研究这个问题，我们不仅可以更好地理解数学与现实世界的联系，还可以发现新的科学和技术应用，我们应该继续探索这个问题，以期发现更多的科学和技术突破。